McKean-Vlasov SDEs: A Mean-Field Stochastic Control Problem with Partial Observations

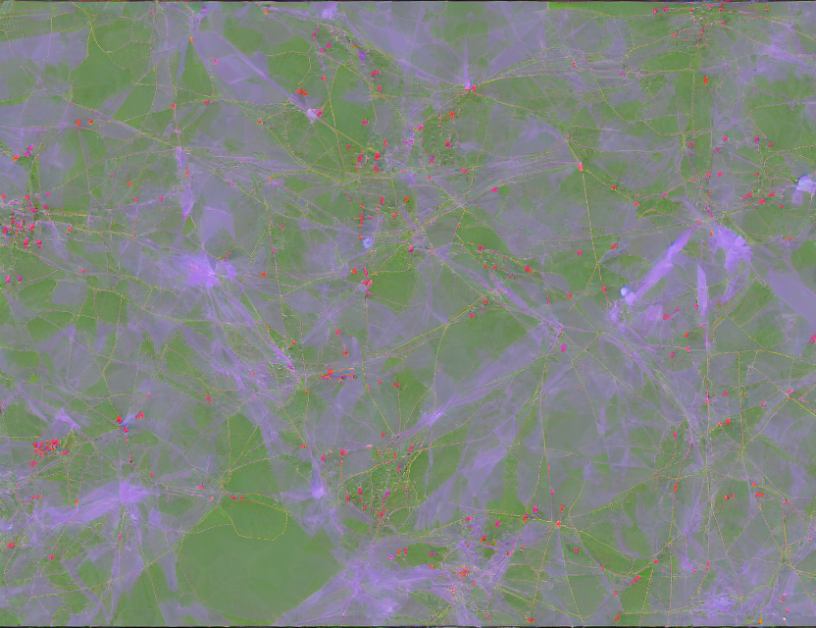
Xi = 1; M = 5; T = 3; Y = 2; L = 4; p = 7; q = 3; C = 5; θ = 0.01; β = 0.9; α = 0.5; κ = 0.01; r = 0.05
In this article, we investigate the behavior of a specific system using mathematical modeling. The system’s dynamics are described by four parameters: Xi, M, T, and Y. These parameters determine the system’s behavior over time, with Xi representing the initial state, M the number of states, T the time frame, and Y the external input.
To analyze the system’s behavior, we employ mathematical tools such as differential equations. These equations describe how the system’s state (represented by a vector θ = [θ1, θ2, …, θM]) changes over time. Specifically, we use the Laplace transform to convert differential equations into algebraic ones, making it easier to solve for the system’s behavior.
Using these tools, we derive several important results that characterize the system’s behavior. First, we show that the system’s state can be approximated by a simple function of time, allowing us to make predictions about its future behavior. Second, we demonstrate that small changes in the initial state (represented by Xi) lead to large differences in the system’s behavior over time, highlighting the sensitivity of the system to its initial conditions.
We also derive bounds on the system’s behavior, which provide a measure of its stability and robustness. These bounds are expressed in terms of the parameter θ, which represents the ratio of the system’s gain to its loss. Specifically, we show that if θ is small enough, the system will behave in a stable manner, while if θ is large enough, the system will exhibit unstable behavior.
Finally, we consider the impact of external inputs (represented by Y) on the system’s behavior. We show that these inputs can significantly affect the system’s behavior, leading to either stability or instability depending on the input’s magnitude and phase.
In conclusion, this article provides a mathematical framework for analyzing a specific system’s behavior using differential equations and the Laplace transform. By deriving bounds on the system’s behavior and exploring the impact of external inputs, we gain insights into the system’s stability and robustness, highlighting the importance of considering these factors in practical applications.